Federated Learning: FedAvg (1/4)

Introduction

In recent years, there has been political and consumer backlash against the constant surveillance of tech companies. In response, companies have turned to federated learning, a technique which enables the training of a single model from decentralized data. Imagine we have $K$ numbered clients. Clients perform the bulk of the computation. Each client $1 \leq k \leq K$ has its own dataset $D_k$, a local model $f_k$, and a loss function $L_k$.

Generally, the local loss functions are sums over the client’s dataset.

Here $\ell(\hat{y}, y)$ is the per-example loss; it measures the difference between the label $y$ and the prediction $\hat{y}$. A server coordinates the learning process; it usually has no data of its own. The goal is to train a global model $f$ which minimizes the total loss $L = \sum_{k=1}^{K} L_k$. For now, we assume all models have the same architecture but different parameters.

Let’s look at some possible applications of federated learning.

• Word completion (McMahan & Ramage, 2017). Smartphone keyboards attempt to autocomplete words based on the characters typed. Each Android phone has its own record of typed characters and the finished word. Because pooling data from millions of phones is invasive and expensive, Google uses federated learning to learn a universal word prediction model.
• Illness prediction. Hospitals are required by law to keep patient information private. However, a group of small hospitals want to use their collective data to train a neural network which can guess ailments based on symptoms. The hospitals decide to use federated learning to learn a collective model without sharing sensitive data.

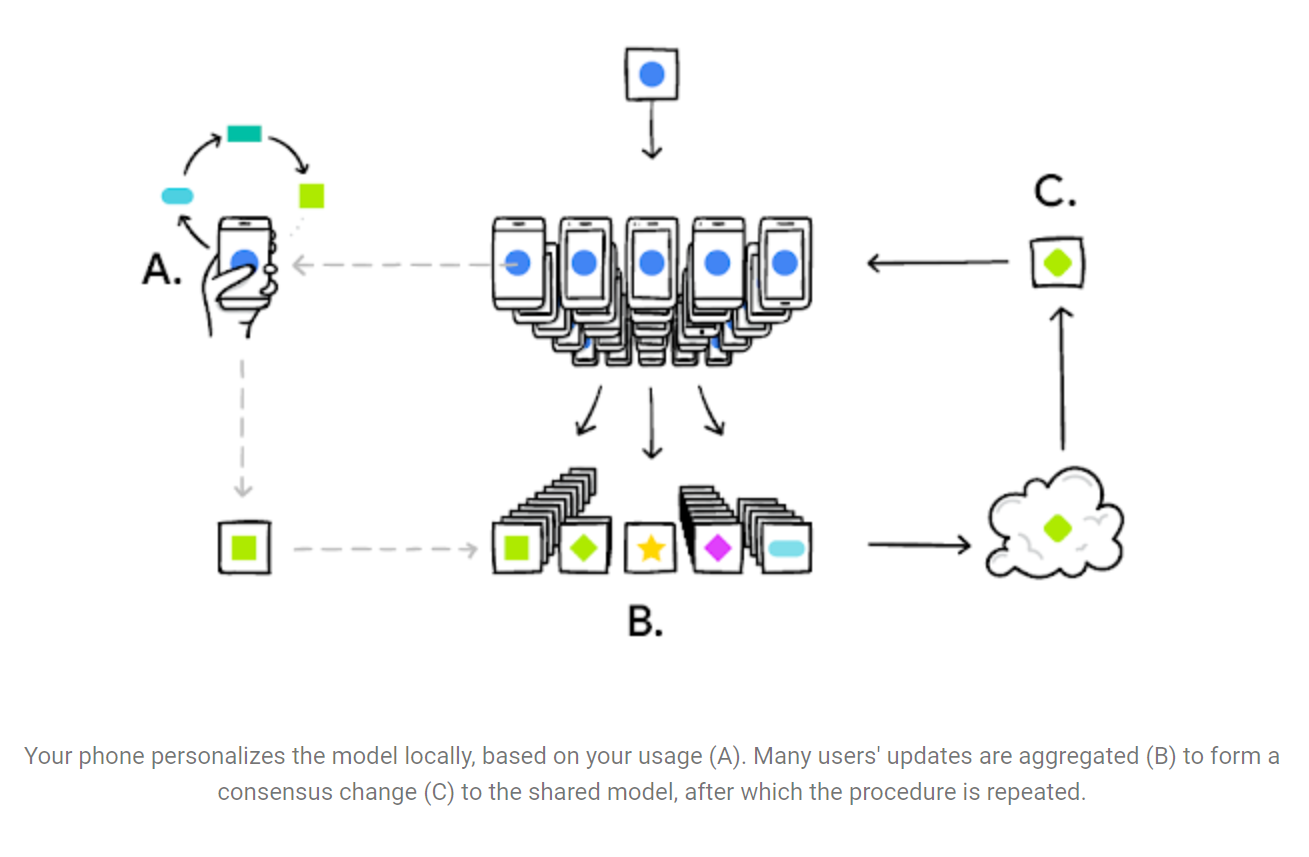
Graphic from (McMahan & Ramage, 2017).

Federated SGD

So federated learning appears to be quite useful. But how exactly do we train a global model without having access to training data? Let’s consider the typical training loop in supervised learning.

epochs = # number of epochs
lr = # learning rate

dataloader = # object that iterates over the dataset
model = # some neural network
optimizer = SGD(model.parameters(), lr=lr)

for e in range(epochs):
    for data, labels in dataloader:
        loss = loss_function(model(data), labels)
        loss.backward()
        optimizer.step()

Recall that the total loss function $L$ is the sum of many different loss functions $L_k$. Taking the gradient with respect to $\theta$ yields

Each client only has enough data to compute $\nabla L_k({\theta})$. However, by having the server add these together, we can know $\nabla L(\theta)$. Thus, FedSGD has each client—more often a randomly chosen subset of all clients—compute its local gradient $\nabla L_k({\theta})$ which are sent to the server for aggregation. The server updates the parameters which are broadcasted to the clients.

rounds = # number of communication rounds

clients = # list of client objects
server = # server object

for t in range(rounds):
    for client in clients:  # do in parallel
        for data, label in client.dataloader:
            loss = loss_function(client.model(x), y)
            loss.backward()

    server.aggregate_gradients(clients)
    server.optimizer.step()
    server.broadcast_params(clients)

Federated Averaging

The problem with FedSGD is the communication cost. Imagine training a neural network to recognize handwritten digits using the MNIST dataset, which has 60,000 training examples. This should only take about 20 epochs—passes through the dataset. With a batch size of 100, there are $60,000/100 \cdot 20 = 12,000$ updates. In FedSGD, each update would require an onerous process of clients computing and sending gradients, aggregation, then the server broadcasting parameters. This is bad, especially considering the ever increasing size of models.

A little bit of math reveals that there might be a solution. Suppose the server uses Stochastic Gradient Descent to update the weights. Let $\eta$ be the learning rate.

Replace $\nabla L(\theta)$ with $\sum_{k=1}^{K} \nabla L_k(\theta)$.

Notice that $\theta$ can be moved inside the sum.

Having the server update the parameters using the aggregated gradient is equivalent to the clients perform the update, then “averaging” the parameters on the server later. If the clients can perform multiple updates, then the server will need to average less frequently, reducing communication costs.

rounds = # number of communication rounds
epochs = # number of epochs

clients = # list of client objects
server = # server object

for t in range(rounds):
    for client in clients:  # do in parallel
        for i in range(epochs):
            for data, labels in client.dataloader:
                loss = loss_function(client.model(data), labels)
                loss.backward()
                client.optimizer.step()

    server.average_params(clients)
    server.broadcast_params(clients)

Convex Loss Functions?

However, neural network loss functions are non-convex in general. So there is no guarantee that averaging (the parameters of) multiple models produces a better model.

Training 2 neural networks from different initialized parameters demonstrates this. The averaged parameters do worse than before. However, this is not the case when training 2 neural networks from the same initialization. In fact, plotting the loss resulting from different weighted averages of the parameters reveals a nice U-shaped graph.

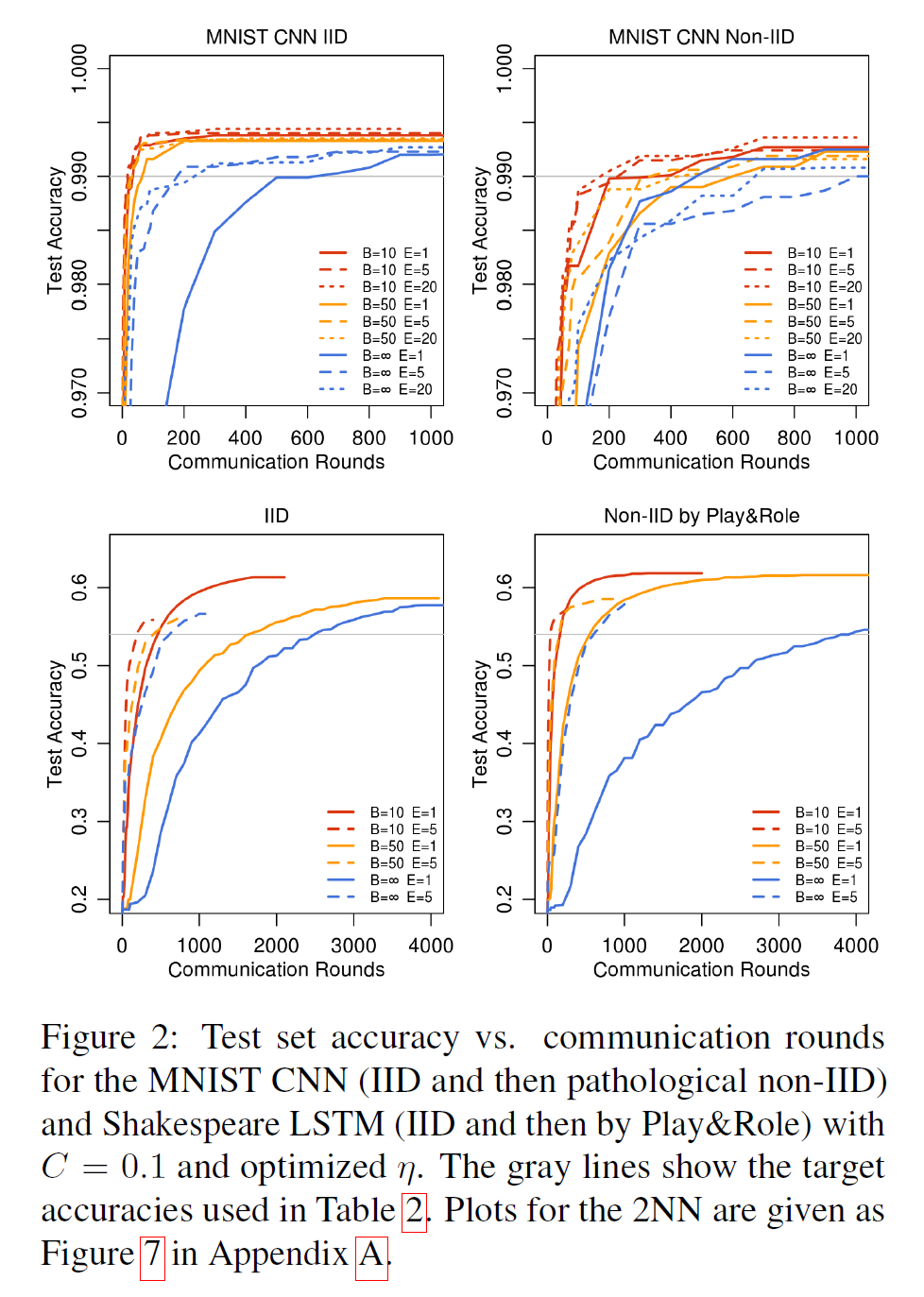
Figure 1 from (McMahan et al., 2017).

Limitations

FedAvg works well when the client datasets are IID—identically and independently—distributed (McMahan et al., 2017). (Note that the accuracy figures are made monotonic. If $a_1, a_2, \dots$ are the actual accuracies, then the plotted value at time $t$ is $\max_{s \leq t}(a_s)$.) Returning to the Illness Prediction example, the hospital’s dataset would be IID if all contained the same types of diagnoses. So hospital A’s dataset cannot consist of mostly flu examples while hospital B has low amounts of flu cases. However, when data is non-IID, it’s performance suffers. In particular, actual accuracy can vary wildly between communication rounds.

Another issue is the number of hyperparameters to manage. There is the proportion of clients which participate each round $C$, the number of epochs $E$, and the batch size $B$. While moderate values of each do fine ($C \approx 0.1, E \approx 5, B \approx 10$), there is a complex interplay between them.

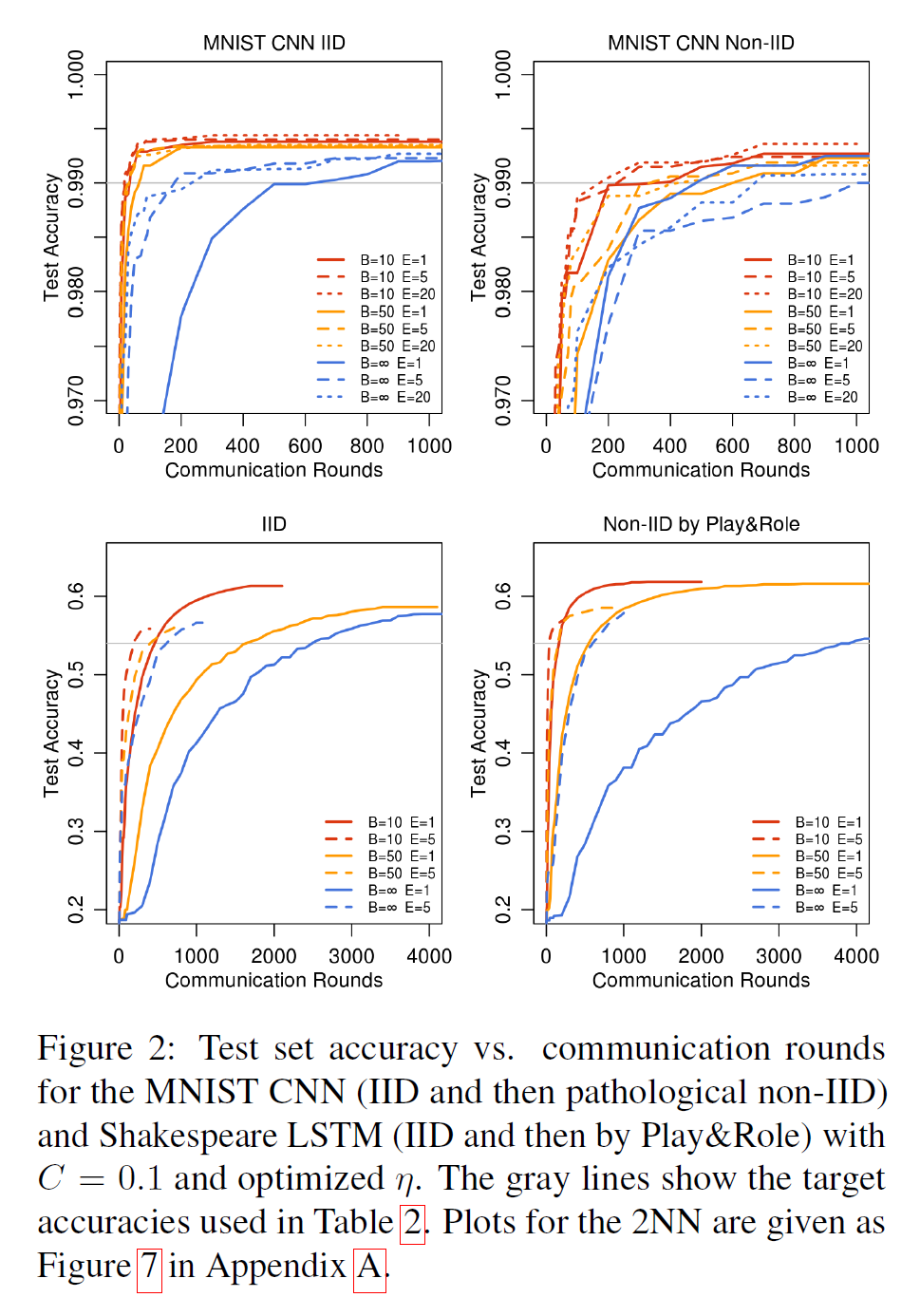
Figure 3 from (McMahan et al., 2017).

Lastly, before averaging, the server must wait for every client to finish $E$ epochs. As clients may have different amounts of hardware, faster clients are now idle while the server waits for slower clients. We might try to amend this by fixing a timed interval during which each client performs local updates. But now the averages are biased—especially in the beginning of training—towards the faster clients. The averaged model will perform better on some datasets than others. Training is uneven.

References

2017

1. McMahan, B., Moore, E., Ramage, D., Hampson, S., & y Arcas, B. A. (2017). Communication-efficient learning of deep networks from decentralized data. Artificial Intelligence and Statistics, 1273–1282.
2. McMahan, B., & Ramage, D. (2017). Federated Learning: Collaborative Machine Learning without Centralized Training Data. http://ai.googleblog.com/2017/04/federated-learning-collaborative.html